Bayesian Decision Theory using Financial Economics Assignment solution

Zackhauser Paradox Problem

1. Zeckhauser’s Problem

The following example casts doubt on the Bayesian view about the uncertain world.

You’ve been kidnapped. You’re rich, and you must pay ransom or face death. If you’re to die, it makes no difference to you if you die rich or poor. Consider two choices:

Case 1. You must play Russian roulette for your freedom, using a six-shooter with two loaded chambers. How much would you pay to empty both chambers before pulling the trigger?

Case 2. If there were only two empty chambers, how much would you pay to empty the third chamber before pulling the trigger?

”Biting the Bayesian Bullet: Zeckhauser’s Problem,” by Richard Jeffrey in Theory and Decision 25 (2):117-122 (1988)

Show that a DM who satisfies the independence axiom must pay the same amount.

Suppose that you pay more in Case 1 than in Case 2 as I would. Then you violate the independence axiom and you cannot be represented by the vNM expected utility function. (Refer to the article posted on BB. It is an interesting article. Please take time to read what he tries to say. The article sounds more like a confession from a person who used to be a believer of human rationality as most economists do. The independence axiom leads to a very unlikely behavior that goes against common sense. )

2. (P-beauty contest and Tulipmania)

(a) In 2 -Beauty Contest game where players pick a number from (1,2,..,100), Explain why the choice 100 by a player is not rationalizable. Explain also why choice 32 by a player is not rationalizable. (Try to show that 32 is the best choice against other rationalizable strategies. You may need to go a few steps of this.)

(b) Using the concept of rationalizable strategies in the 2 -Beauty Contest game, explain why the behavior of the investors in Tulipmania is irrational.

3. (Scared by a test result)

We may be misled by our perception regarding a probabilistic assessment of a situation. A probabilistic assessment has no meaning if we do not have the underlying information about the population to which the accuracy of the assessment is applied.

Suppose that 100 out of the total population of 1 million have a rare form of cancer. A test is 99% accurate in detecting cancer. Now suppose that a person’s test turns out to be positive that he has cancer. What do we conclude from this? Does it mean that the person has cancer with 99% chances?

(A test is 99% accurate if the following holds. If one has cancer, then the test will be ”positive” with a probability of 0.99 and will falsely be ”negative” with a probability of 0.01. If one does not have cancer, then the test will be ”negative” with a probability of 0.99 and will falsely be ”positive” with a probability of 0.01.)

(1) Draw the Venn diagram

To do this question, assume the whole population is tested, and find the numbers for the following.

1. Those who have cancer
2. Those who are positive
3. Those who have the disease and the test correctly show positive. 100 x (99/100)=99
4. Those who do not have the disease and the test incorrectly shows positive 999,900 x (1/100)=9999
5. Those who do not have the disease and the test correctly shows negative
6. Those who have the disease and the test incorrectly show negative

(2) Use the direct method to find the answer

(3) Also use the Bayesian updating to find the answer

4. Two bidders, B1 and B2, participate in a Vickery auction (the second price sealed bid auction) by submitting bids, b1, and b2, where the winner pays the price equal to the second-highest bid. The values of the object for B1 and B2 are given by v1 = 100 > v2 = 60. If the bids are tied, then B1 receives the object and pays the price as described above.

(1) Find the best response function for B1 and B2

(2) Find the Nash equilibrium

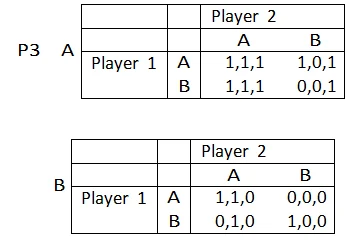
5. The three-player game is shown below. We know that (B, A, A) is a Nash eq. Show that it is not a trembling hand perfect Nash eq.

6. (War of Attrition) Suppose that two firms, A and B, are fighting to push the other out of business. If a firm exits the market, then the other firm becomes the monopolist. The fighting costs each firm c dollars per unit time.

If the fighting lasts t units of day, then the cost is given by ct. The longer the game lasts, or the longer both do not concede, the higher the cost will be.

The profit Firm A receives as a monopolist is 4 and the profit Firm B receives as a monopolist is 6. Let tA is the concession time for A and action tB is the concession time for B.

The payoff for A is given by

uA(tA, tB) = −ctA if tA < tB

= − ctA if tA = tB

= 4 − ctB if tA > tB

The payoff for B is given by

uA(tA, tB) = −ctB if tA > tB

= 2 − ctB if tA = tB

= 6 − ctA if tA < tB

Find the best response function for A. Find the Nase Eq.

7. Two Cournot duopoly firms, facing a demand P (q1, q2) = 90 (q1 +q2), simultaneously choose their levels of output to maximize profit. Suppose both firms have the same unit cost

6. Show that successive elimination of strictly dominated strategies yields a unique prediction (q1, q2) = (28, 28) in this game.

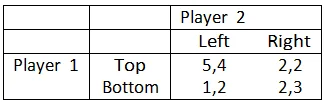
8. Find the best response functions. Find all the Nash equilibria (including the mixed strategy Nash eq.).

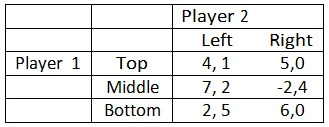
9. Consider the game below.

(1) P1’s strategy ”Top” can never be the best response. True or False? Show why. Your mark depends on your explanation.

(2) P1’s strategy ”Top” is a dominant strategy. True or False? Show why. Your mark depends on your explanation.

10. (Median Voter). 3 people, P1, P2, and P3 have to collectively pick one policy, say tax rate. Each person i has a best policy, x1∗ = 0.2, x∗2 = 0.5, x3∗ = 0.7 for P1, P2 and P3. The farther away from xi∗ the policy is, the less preferred. And the median of the announcements among a1, a2, and a3 is selected. For example, if a1 = 0.5, a2 = 0.9 and a3 = 0.1, then

0.5 is the chosen policy. Find the best response function for P2 for the cases where no two announcements by P1 and P3 are the same, i.e., a1 /= a3.

Solution:

1.ZECKHAUSER’S PROBLEM

Let us calculate the expected utility in both cases. In case one, there are two chambers that are loaded. In case two, there are four chambers that are loaded. If D is death, and L is life, then the utility function becomes u(D) = 0 and u(L) = 1. The general form of the equation is:

u(Ak) = k u(D) + 6−k u(L)

If we let A1 be the event that you pay the maximum sum you are willing to pay, then that means you are indifferent between A1 and 2 D + 4 L. So the function becomes:

u(A2) = 2 u(D) + 4 u(L) = 4

For case two we have the function become:

1 u(D) + 1 u(A4) = 4 u(D) + 2 u(L) = 4

2 2 6 6 6

u(A2) = u(A4). This shows that you would be willing to pay the same amount in both cases when the independence axiom holds, as the utilities in both cases are the same.

2. P-BEAUTY CONTEST AND TULIPMANIA

Choice 100 is not rationalizable because the aim is to pick a number that is two-thirds of the average of the numbers picked. Suppose that everybody picks the maximum number, which is 100, then the winning number must be two-thirds of that. Or roughly 67. So therefore any number from 67 to 100 should never be picked. Choice 32 is also not rationalizable. This is because any rational agents would quickly see the nash equilibrium as

0. We follow a similar line of reasoning. If 67 is the highest number anyone would rationally pick, then the winning number must be two-thirds of that, or 44. We can keep this going as well. If 44 is the highest number anyone would rationally pick then the winning number would be two-thirds of that, which is 30. We see that 30 is below 32, and so 32 should not be picked. The behavior of investors during tulip mania was irrational for similar reasons. Tulips were bought with the expectation that the selling price would be higher than the buying price. This obviously cannot continue forever, as eventually, the prices would be so high that nobody would have the physical wealth to buy them. This is how the market collapsed. People realized they did not have the money to pay for tulips and overnight the market collapsed.

3. SCARED BY A TEST RESULT

1. The number of people who have cancer is 100
2. Those who are positive is 100 ∗ (99/100) + 999900 ∗ (1/100) = 99 + 9999 = 10, 098
3. 100 * 99/100 = 99
4. 999,900 * 1/100 = 9999
5. 999,900 * 99/100 = 989,901 f) 100 * 1/100 = 1

Suppose the value for B1 and B2 is given by v1 and v2. suppose that b1, b2 ¿ v1, v2. There are three possible outcomes. βˆ is the highest bid of the other bidder. First, βˆ ¿ b1, v1. Second, b1 ¿ ˆb ¿ v1. Finally, b1, v1 ¿ ˆb. In the event of the first or third outcome, 1 would have done equally well to bid v1, rather than b1 ¿ v1. In scenario 1 they don’t win regardless, in two, they win and pay ˆb, though they will pay more than their value. So it is better to bid v1 than b1 ¿ v1. So this shows that the nash equilibrium is truthful bidding.

This is not a trembling hand perfect nash equilibrium because equilibria are both weakly dominant. For trembling hand perfect nash equilibria we need that there be no weakly dominant strategies.

6. WAR OF ATTRITION

The best response function for A is to quit. This is because in the case where TA = TB, 4 < 6, which maximizes the profit to both players. If A stays in the game until the end, then the maximum profit B can get is 2, which is less than they would get if they quit immediately at the same time as A. So the best strategy is for both players to quit immediately and maximize their profit.

7. COURNOT DUOPOLY

Suppose we focus on Player 1. Their payoff is:

(90 − q1 − q2)q1 − 6q1

= 84q1 − q12 − q1q2

Player one maximizes profits when the first-order conditions are met. Which are:

q1 = 84−q2

And so player one never chooses a value more than 42. Iterating this down, we can come to the unique equilibrium of 28 for both players. This occurs after the second set of eliminations for both strategies.

8. NASH EQUILIBRIA

The Nash equilibria in this game are Top Left, Bottom Right. The mixed nash equilibria are Top Right.

9. BEST RESPONSE

The top is the best response for Player one as this produces the best results for them. Their expected value is 4.5. The expected values for them are 2.5 for the middle and 4 for the bottom. This is also why the top is a dominant strategy for them. Any other option reduces their utility.

10. MEDIAN VOTER

The best response function for two is:

BR = (x2 : —x2 - m— ¡ —x1,3 - m—). So we see that there is no nash equilibrium if anybody chooses m. The only unique nash equilibria is if all players choose m. Though if a1 and a3 are not the same then this does not occur. Therefore The best response of P2 is to play a truthful game, as they will generally be in the median of the announcements.