Game Representations and Static Games
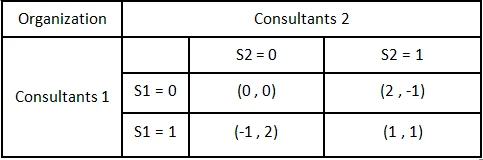
- There are two cyber security consultants, i=1,2 who share cyber threat intelligence (CTI) with each other to protect an organization. Each can decide to share (si=1) or not share (si=0). The total profit of the organization is 4(s1+s2) and is shared equally between the two consultants. Each consultant incurs private cost 3 when sharing and 0 when not sharing. Show the single-stage strategic form of this game. Is there a natural prediction of how this game would be played between these consultants in this static single-stage game? Comment on the outcome of the game solution.
- If a cyber security firm decides to create generic firewall rules for their server protection (with information worth of “P”), they have a risk of losing “c” (information worth of “c”) to the attacker. In other words, if they create generic firewall rules, the effective payoff for the cybersecurity company would be “P-c.”
- Present the game between cybersecurity firm and privacy inspector in its strategic form. Explain each component.
- Based on what conditions and relationships between “c,” “f,” and “ρF,” does the cybersecurity firm have a dominant strategy in this game? What is that dominant strategy? Explain and show your steps clearly.
- Based on what conditions and relationships between “c,” “f,” and “ρF,” does no player in this game have a pure dominant strategy? What would be the equilibrium strategy in that case? How would you obtain that? Explain and show your steps clearly.
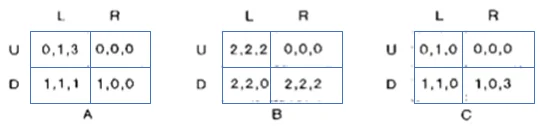
- In the game illustrated below, there are three players. Player 1 chooses rows, player 2 chooses columns, and player 3 chooses matrices. Accordingly, in the utility tuple, the first value represents player 1’s utility, the second value is player 2’s utility, and the third value is player 3’s utility. Is there any equilibrium existing in this game? If so, find it and explain the process for finding it.
However, if they decide to do profiling of any incoming user and collect their personal information, they may develop a much stricter firewall policy and will no longer lose the “c,” but this will also give rise to privacy violation risk. If they are assessed by an inspector, they will be fined “f,” which will go toward the inspector. Further, by collecting personal information, there is a risk probability “ρ,” that if this personal information is stolen, the firm will face a lawsuit of cost “F” (the effective expected lawsuit cost is = probability of loss x value of loss = “ρF”).
From the privacy inspector’s side, inspecting the firm costs the inspectors “k,” not inspecting a firm that violated privacy and got caught in the lawsuit, costs “B” in terms of damage done to the inspector's reputations and careers.
Solution:
The couple will be represented as (Consultants1, Consultants2).
When
- if Ci (si=0) and Cj (sj=1) then Ci = 2.
- if Ci (si=0) and Cj (sj=0) then Ci = 0.
- if Ci (si=1) and Cj (sj=1) then Ci = 1.
- if Ci (si=1) and Cj (sj=0) then
Ci =-1. where:
i,j : 1,2 or 2,1. C : consultant.
- Sharing (si = 0) is the rational strategy because when Ci share, Cj will always have the opportunity to not share.
Therefore the only reasonable solution for Ci, i= 1,2, is to play it safe and not share thus (0,0).
The couple will be represented as (privacy Inspector, Cybersecurity firm).

No, based on what conditions and relationships between “c,” “f,” and “ρF,” the cybersecurity firm doesn’t have a dominant strategy in this game.
Explanations:
- If the privacy inspector is not inspecting the cybersecurity firm have P-pF as value.
- If the privacy inspector is inspecting the cybersecurity firm will have a P-f-pF as value and it is better only if pF+f < c.
Yes, Based on what conditions and relationships between “c,” “f,” and “ρF,” no player in this game have a pure dominant strategy.
The Nash equilibrium strategy is: (0, P-c) when the privacy inspector is not inspecting and the Cybersecurity firm is using a generic firewall.
This case satisfies the definition of the Nash equilibrium. A Nash equilibrium is a law that no one would want to break even in the absence of an effective police force.
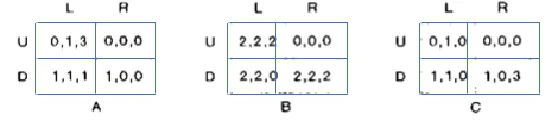
Yes, there is an equilibrium which is (2,2,2).
The process of finding the equilibrium is by elimination of strictly dominated strategies, and we can clearly see that when player 1 chooses Down, player 2 chooses Right, and player 3 chooses matrice B, there are no better choices for any player.
Related Samples
Explore our diverse array of sample materials specifically crafted for students studying game theory. These resources present a plethora of practical scenarios illustrating core game theoretic concepts, strategic interactions, decision-making analyses, and behavioral dynamics. Immerse yourself in these samples to uncover profound insights into the intricate world of game theory and its real-world applications.
Game Theory
